POGIL 1 - SIS Model

Introduction

This POGIL was created by Eric Araújo (eric.araujo@calvin.edu) and is mostly based on the model from section 4.5 of the book Modeling Social Behavior by Paul E. Smaldino.

This activity will guide you through creating a SIS model for the contagion of transmissable diseases.

Student Learning Objectives: At the conclusion of this activity, students will be able to:

Understand what is the SIS contagion model.
Implement the agent-based model version of SIS.
Understand the equation-based model for a SIS model.

Prerequisites: students should have some understanding of Netlogo programming and Behavior Space, provided in Project 2.

Process Skills Goals: Students will exercise:

their capacity to implement a contagion model in Netlogo.
handling more complex models with equations and using agents.

Before you start, complete the form below to assign a role to each member. If you have only 3 people in your group, combine Presenter and Reflector.

Date
Team Roles	Team Member
Manager: reads the questions aloud, keeps track of time, and keeps the team moving quickly.
Presenter: talks to the instructor and other teams.
Recorder: records all answers & questions, and provides team reflection to team & instructor.
Reflector: Considers how the team could work and learn more effectively. Slows down the team if everyone is not understanding the answers.

1. Description of the SIS Model

Assignment Introduction: Expanding the SI Model

In the SI (Susceptible-Infected) model discussed in class, we made a simplifying assumption: once individuals become infected—or adopt a product, behavior, or idea—they remain in that state indefinitely. While this assumption simplifies the model, it doesn’t always reflect real-world dynamics.

In reality, many infections resolve over time, allowing individuals to recover and return to a healthy state. Similarly, in the context of products or behaviors, people often change their minds. They may stop using a product, abandon a behavior, or decide an idea no longer suits them. This change may be permanent, or it could be temporary—a hiatus after which they may return to a susceptible state.

For this assignment, we will explore this latter scenario, where individuals can recover or disadopt and then become susceptible again. This adjustment will allow us to examine a more dynamic and realistic representation of social or biological processes.

Important

Just a reminder, the equation for the SI model is

\(I_{t+1}=I_t+\tau I_t\big(1-\frac{I_t}{N}\big)\)

Key Assumptions of the Model

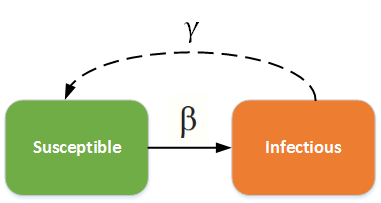
The figure above shows the susceptible-infected-susceptible structure. In this new scenario, infected individuals recover with a fixed probability for every unit of time they are infected. That is accounted by the parameter \(\gamma\), meaning that each time step there is a proportion \(\gamma\) of infected individuals (I) that move back to the susceptible group (S).

Considering \(\tau\) as the rate of people getting infected per time step, we can say that the number of infected people next time step will be the total number of people infected at this time step plus the number of people who are not infected and will become infected at a \(\tau\) proportion, minus the proportio \(\gamma\) of individuals who will recover.

🔑 Write down this equation and report it to the blackboard. I will keep the answer at the footnote of this page¹. Do not look at the answer until you report!

In this extended model, we introduce a new dynamic: at each time step, susceptible individuals can become newly infected, while infected individuals may recover and return to a susceptible state. This interaction creates a balance—if the contagion spreads effectively, the population will settle into an equilibrium where the rate of new infections equals the rate of recovery.

Unlike the SI model, where the entire population eventually becomes saturated with the contagion, this updated model maintains a dynamic equilibrium. A fixed proportion of the population remains infected at any given time, even though individuals continuously change their infection status. This concept of equilibrium is central to understanding more realistic contagion dynamics and forms the basis for this assignment.

When is this equilibrium reached? What are the conditions necessary for it to happen?

So we can use a mathematical equation to calculate the precise moment when the population getting infected is in balance with the population recovering. That is, when \(I_{t+1}=I_t\). In this case, we can ommit the subscripts as there is not change from time \(t\) to time \(t+1\).

🔑 Starting with the equation reported in question 1, are you able to rewrite it considering that \(I = I_{t+1} = I_t\)?

You should get a result like the one shown in the footnotes². Resist the temptation to look at it until you come up with a solution.

Your result should be showing that the equilibrium depends on a ration between \(\gamma\) and \(\tau\). And that makes sense. When the proportion of people getting infected is the same as people recovering, you will have the same amount of individuals moving from S to I and vice-versa.

2. Coding the model

Open up the SIS NetLogo model provided in the following link: https://github.com/ericaraujophd/agentmodeling/tree/main/code/week02.

Take some time to play with the code and understand what it is doing.
To modify this model into a SIS model, we first need to add a new stage before recoloring the nodes called recovery. In this stage, infected agents may recover and become susceptible again. But we have one problem in here:

During this stage, infected agents may recover and become susceptible again. Importantly, we don’t want a new infection to be immediately negated by having a newly infected agent recover before the agent has the opportunity to infect its neighbors (or, more importantly, before it has actually been infected for any amount of time). Here is where careful consideration of one’s code is crucial. If we use only the value of an agent’s infected? parameter, an agent could flip from susceptible to infected and back to susceptible on a single time step. One way to avoid this is to use two different markers of agent infection. Luckily, we already have this redundancy built into our code, since an agent’s infection status is represented both by the Boolean variable infected? and by the agent’s color. If newly infected agents remain white until the end of the time step, we can restrict recovery to agents who are both infected and red. (From Page 99 of the book)

How this problem translates into your code?
🔑 Add the following procedure to your code and make sure it is called in the right place. Report the line in your code where the recover-infecteds procedure should be called in the blackboard.

to recover-infecteds
    ask turtles with [infected? and color = red]
    [
        if random-float 1 < recovery-rate [
            set infected? false
        ]
    ]
end

Your code is supposed to throw and error. Why is that?

Create a slider for recovery-rate from 0 to 1 in your interface.
🔑 Change the stop condition for your model so it will stop when there are no individuals infected. Write that line of code in the blackboard.

Tip

The stop condition from the SI model is that all agents are infected.

Create a monitor showing the number of agents infected per time step.
Run your simulation for around 3400 time steps for num-turtles = 200, speed = 0.5, turning-angle = 360, transmissibility = 0.1, and recovery-rate = 0.02. Can you explain the results? Discuss what is shown in the plot.
🔑 Create a scenario where the spread of the infection doesn’t succeed. Report the values of your parameters in the blackboard.
Think of a batch run using Behavior Space where you could verify how the many combination of parameters causes your model to find an equilibrium or not. How would that work?

Footnotes

\(I_{t+1}=I_t+\tau I_t\big(1-\frac{I_t}{N}\big)-\gamma I_t\)↩︎
\(\tau I\big(1-\frac{1}{N}\big)-\gamma I = 0 \Rightarrow \frac{I}{N}=1-\frac{\gamma}{\tau}\)↩︎