W₂: Contagion

CS300b – Agent Modeling

Eric Araújo

Week 2 – Contagion

Scene of the movie Outbreak (1995).

Contagion

• The spread of contagions is a significant area of research across various fields.
  • Epidemiologists and ecologists study disease spread.
  • Social scientists focus on the spread of ideas and behaviors.
  • Marketers analyze product and innovation adoption.

Contagion

• We will explore contagion dynamics.
  • It primarily uses agent-based models (ABMs) but also introduces mathematical models.
  • This dual approach aims to provide a comprehensive understanding of contagion phenomena.

Diffusion of Innovations

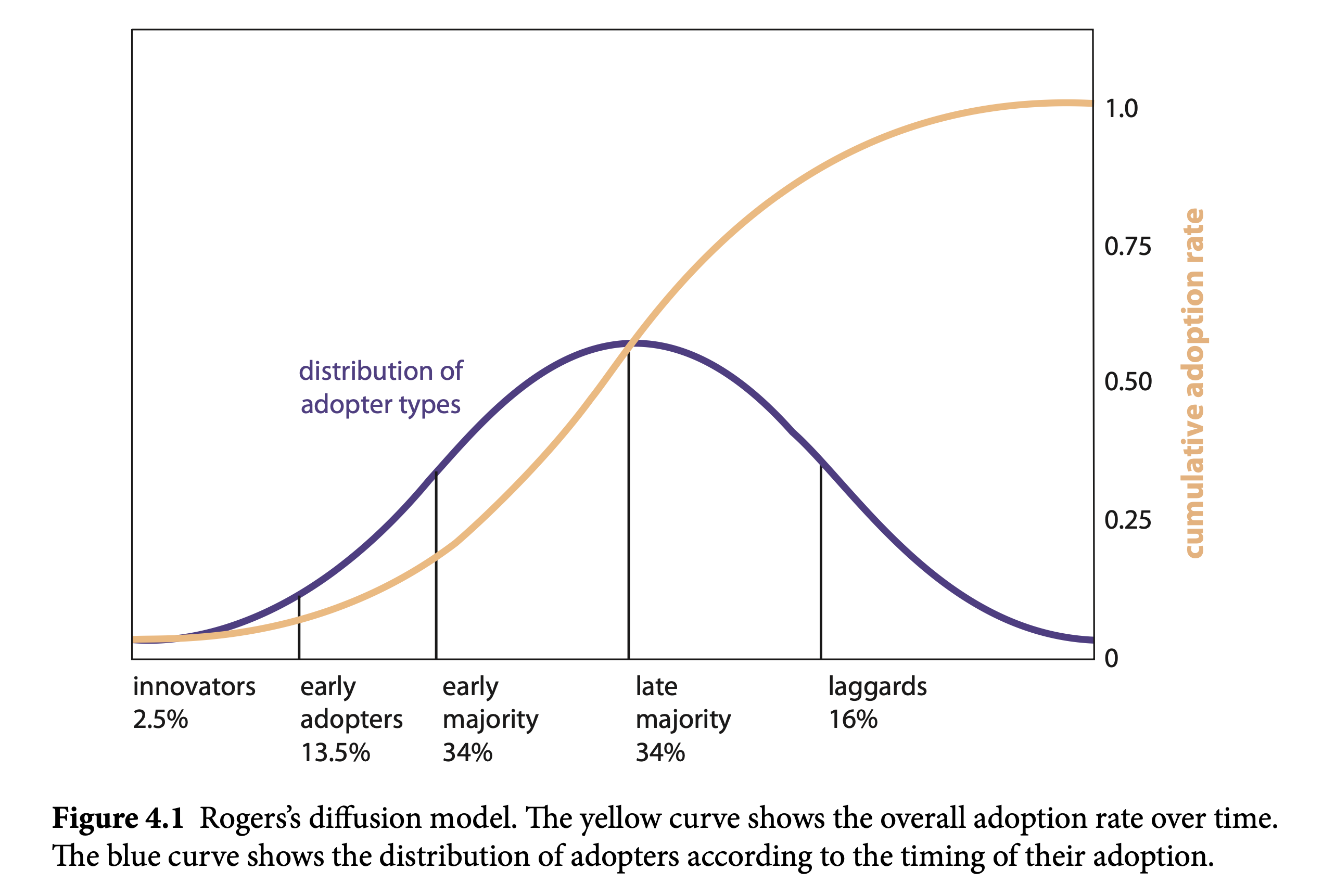
Diffusion of Innovations

• Spontaneous Adoption Model:
  • N is the number of agents.
  • This model assumes a fixed probability (\(\alpha\)) of individuals adopting an innovation per unit time.
  • The change in the number of adopters (\(\Delta I\)) is proportional to the product of \(\alpha\) and the number of potential adopters:
    • \(\Delta I = I_{t+1} - I_t = \alpha(N - I_t)\).
  • This model can be simulated in NetLogo or solved analytically.

Social Influence: The SI Model

• The SI model incorporates social influence alongside spontaneous adoption.
  • Individuals can become infected (adopt) through contact with infected individuals.
  • The rate of infection is determined by the transmissibility rate (\(\tau\)).
  • The discrete-time SI model can be simulated in NetLogo.

Social Influence: The SI Model

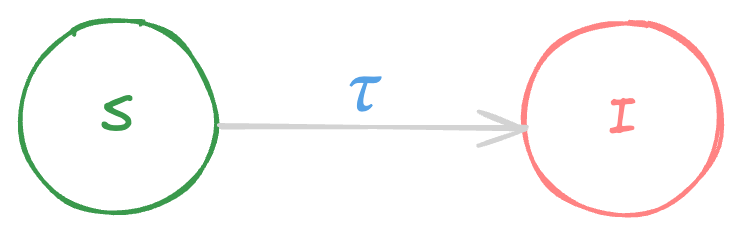
The SI Model - Analytical Model

Because individuals meet at random, the probability of a susceptible person meeting an infected person is given by:

\(Pr(S,I)=\frac{I}{N}\big(\frac{N-I}{N}\big)\)

Therefore, the chance of infection is given by:

\(Pr(infection)=\tau Pr(S,I)\)

\(Pr(infection)=\tau \frac{I}{N}\big(\frac{N-I}{N}\big)\)

The dynamics of infections are given as follows:

\(I_{t+1} = I_t + N \tau \frac{I_t}{N}\big(\frac{N-I_t}{N}\big)\)

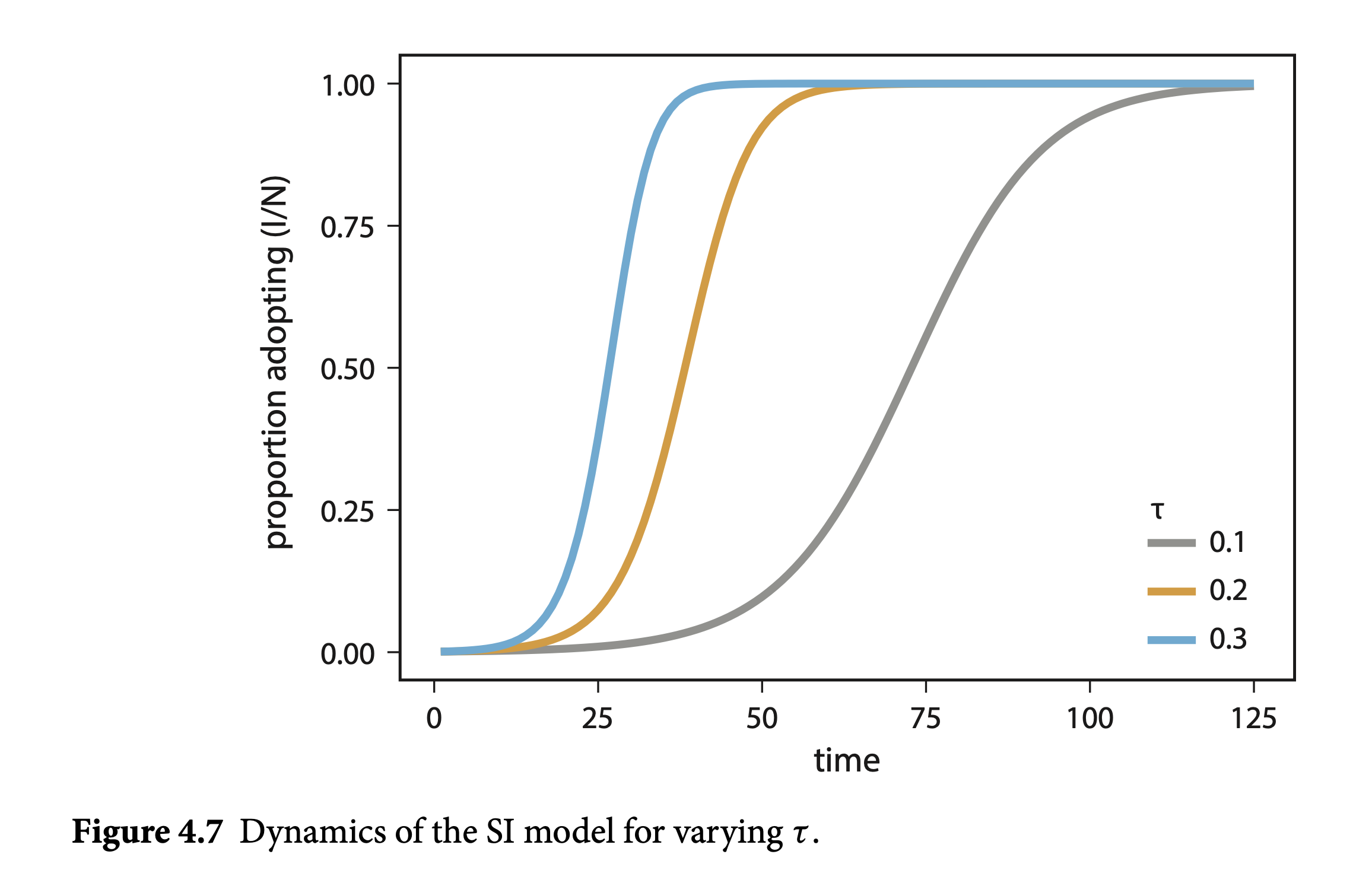
The SI Model - Analytical Model (simplified)

\(I_{t+1} = I_t + \tau I_t\big(1-\frac{I_t}{n}\big)\)

The SI Model - ABM

Transmissibility is caused by multiple neighbors who are infected at a rate of infection \(\tau\).

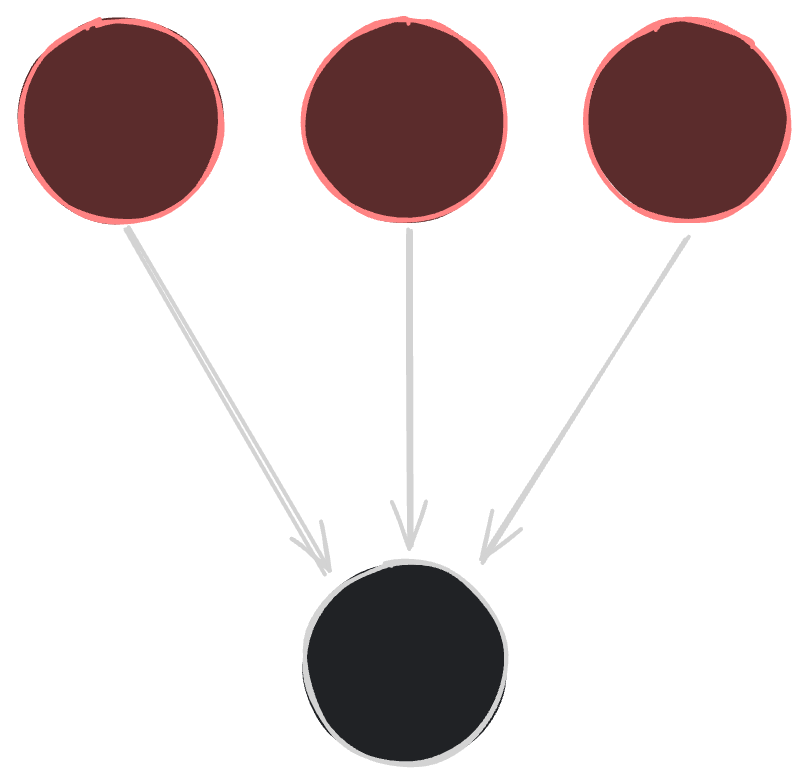
\(Pr(infection)=1-(1-\tau)^n\)

Each infected agent has a chance of \((1-\tau)\) of not infecting the grey agent.

The SIS Model

• The SIS (susceptible-infected-susceptible) model adds recovery to the SI model.
  • Infected individuals recover with a fixed probability (\(\gamma\)) per unit time.
  • The SIS model explores the balance between infection and recovery.

The SIS Model

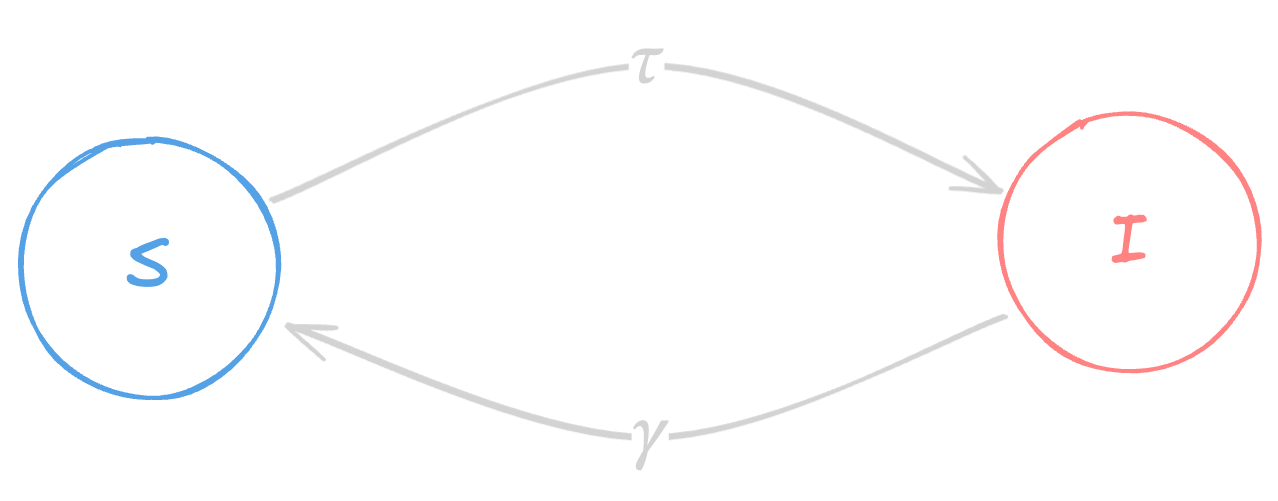
\(I_{t+1}=I_t+\tau I_t\big(1-\frac{I_t}{N}\big)-\gamma I_t\)

The SIS Model - Equilibrium

Dynamic equilibrium happens when the number of people getting infected equals the number of people getting recovered – \(I_t = I_{t+1} = I\).

\[I = I + \tau I\big(1-\frac{I}{N}\big)-\gamma I\]

\[ \boxed{\frac{I}{N} = 1 - \frac{\gamma}{\tau}} \]

\(R_0\) and Herd Immunity

\[R_0 = \frac{\tau}{\gamma} > 1\]

• R-naught or basic reproduction number
• Social and behavioral measures can change \(R_0\).

\(R_0\) and Herd Immunity

\[\frac{\tau}{\gamma}(1-V) > 1\]

• V is the proportion of vaccinated people.
• This is the threshold vaccination rate for herd immunity:

\[V^* = 1 - \frac{1}{R_0}\]

The SIR Model

• The SIR (susceptible-infected-recovered) model incorporates permanent immunity or removal.
  • Recovered individuals are no longer susceptible to infection.
  • The SIR model is often used to study epidemics with lasting immunity.

The SIR Model

• \(\Delta S = -\tau S\frac{I}{N}\)
• \(\Delta I = \tau S\frac{I}{N} - \gamma I\)
• \(\Delta R = \gamma I\)

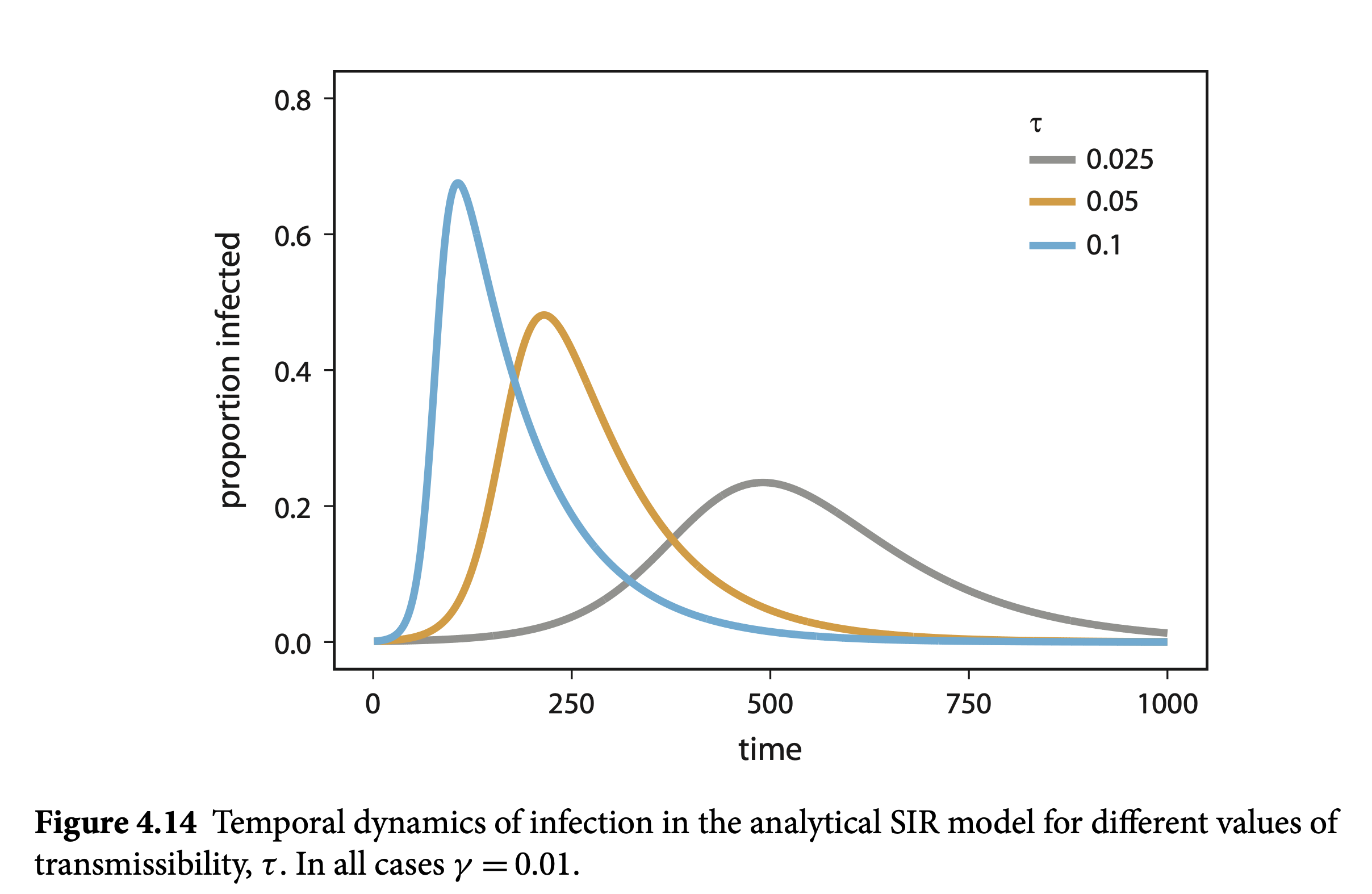
Flattening the Curve

• The SIR model illustrates the concept of “flattening the curve”.
  • Reducing transmissibility (\(\tau\)) through interventions like social distancing can lower the peak infection rate.
  • This prevents overwhelming healthcare systems and provides time for treatment development.

Flattening the Curve

Limitations of Simple Contagion Models

• We must ackwnoledge the limitations of the presented models.
  • Individual variation in transmission, adoption, and recovery is not considered.
  • Models assume random interactions, ignoring population structure and mobility patterns.
  • Cultural norms, socioeconomic factors, and identity are not accounted for.

Simple vs. Complex Contagion

• Simple contagions, like diseases, spread through single contact.
• Complex contagions require multiple contacts for adoption, often involving social reinforcement.
  • This concept was introduced by Centola and Macy (2007).
  • Examples include the spread of certain behaviors, beliefs, and innovations.

Compartment Models

• The SI, SIS, and SIR models belong to a family of models known as compartment models
  • The groups of individuals are compartmentalized in the different categories each model provides
  • There are limitations!