Objectives¶
In this exercise, you will:
Complete a linked-node-based binary search tree class.
Practice building recursive operations.
Practice thinking recursively.
Introduction¶
Today’s exercise is to complete a class template named BST from which binary search tree classes and objects can be created. The exercise provides you with a test-class and a partially-built BST class template; your task is to complete the BST class template.
Getting Started¶
Accept the invitation from github classroom and use git clone, as usual.
Edit the README.md file to add both your names and your partner’s, and make sure you are in the same Team.
The BST Constructor¶
As you can see, our BST class contains just two instance variables:
Node* myRoot; // pointer to the first item we insert
unsigned myNumItems; // number of items I containIn the default constructor, our BST is empty, so myRoot should have the value nullptr and myNumItems should equal zero.
Compile the project and run the tester. The tests should pass.
The insert() Method¶
Looking at the code, your BST class provides methods to:
Create an empty BST;
Determine whether a BST is empty or not;
Determine the number of items in a BST;
Reclaim the dynamic memory of a BST; and
Traverse the tree using preorder.
Our next task is to be able to insert items into a BST. The insert(it) method adds an item it to the tree by storing it in a node such that:
all nodes to the “left” of the node containing it contain items that are less than it; and
all nodes to the “right” of the node containing it contain items that are greater than it.
Note that if we use a simple approach to insert() in which the first item is stored in the root node, the second item is stored in a child node of the root node, and so on, then the order in which we add items can make a big difference in the shape of the tree. For example, if we insert items in a “carefully chosen random” order: 44, 66, 22, 55, 11, 77, 33, then our tree will be balanced:
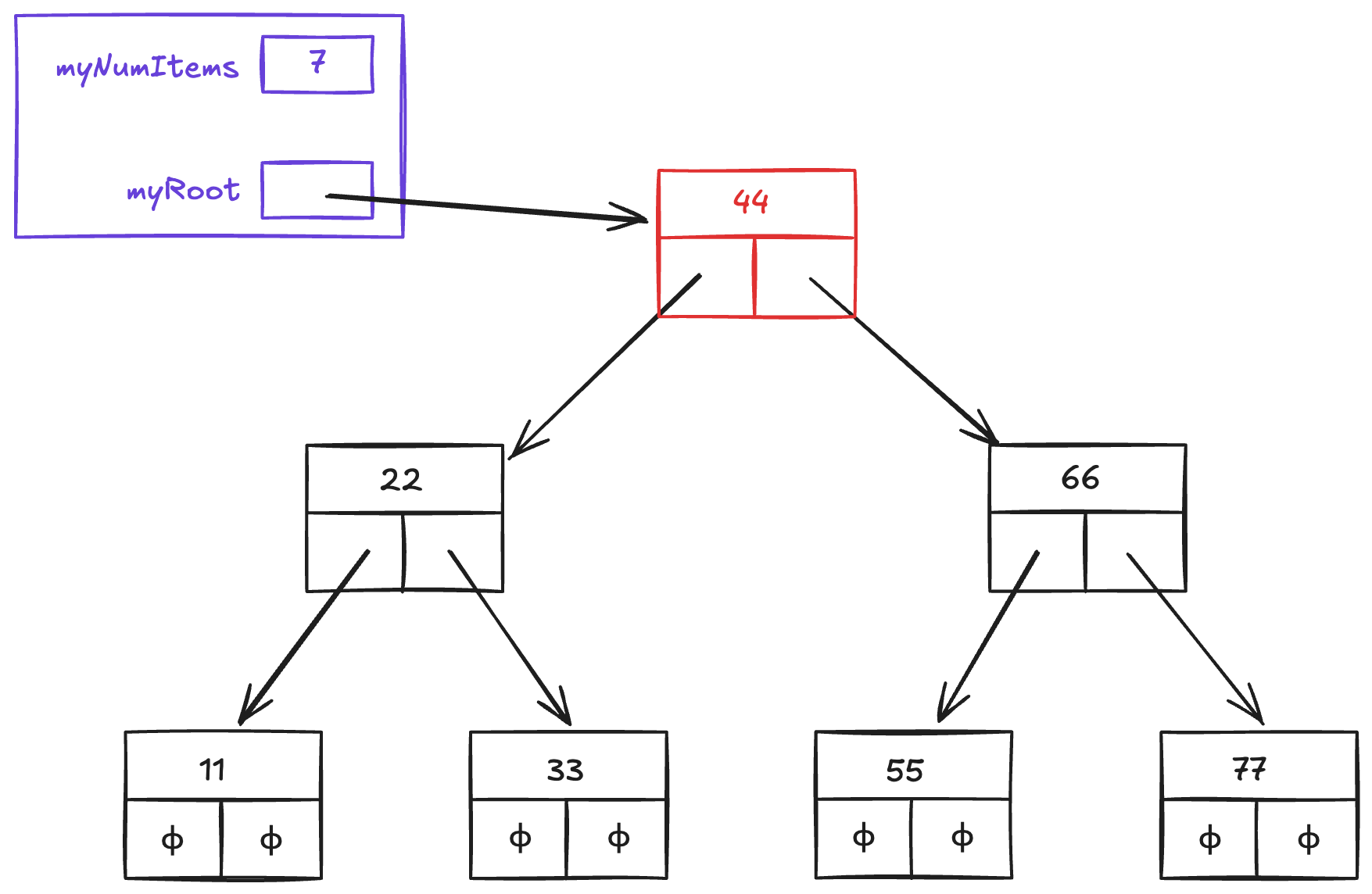
Figure 1:Balanced tree after inserting 44, 66, 22, 55, 11, 77, 33
A tree’s shape can be characterized in different ways. One way is by comparing its height, diameter, and maximum width:
A tree’s height is the number of nodes on the longest path from the root node to any of the leaf nodes.
A tree’s diameter is the number of nodes on the longest path between any two leaves in the tree. This path often includes the root node, but not necessarily.
A tree’s maximum width is the largest number of nodes on any given level of the tree.
The preceding tree’s height is 3, its diameter is 5, and its maximum width is 4. If a binary search tree is balanced, then its height should be about , where is the number of items in the tree.
By contrast, if we insert items in ascending order: 11, 22, 33, 44, 55, 66, 77, then our tree will be imbalanced one way:
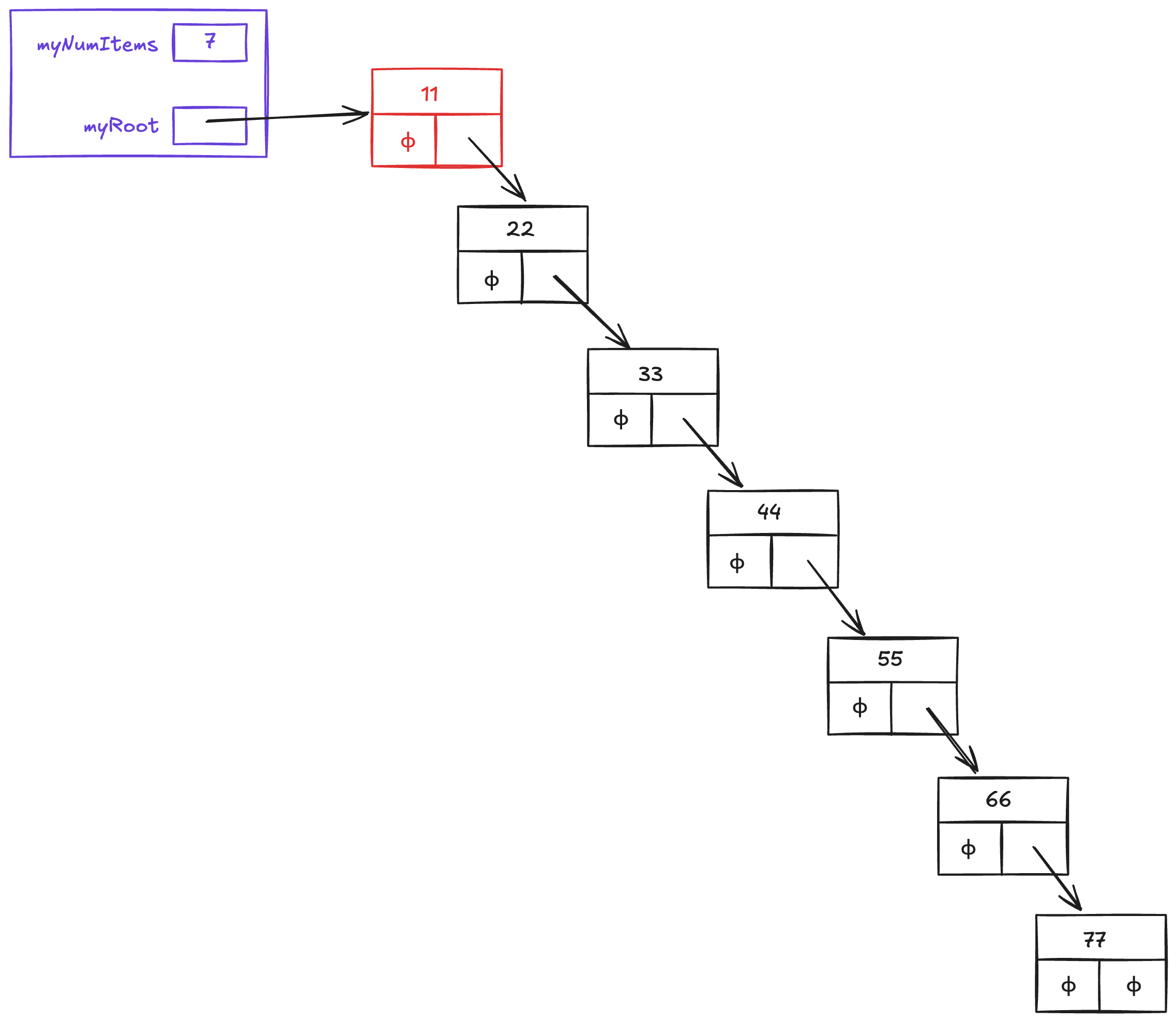
Figure 2:Imbalanced tree after inserting 11, 22, 33, 44, 55, 66, 77
This tree’s height is 7, its diameter is 7, and its maximum width is 1.
Likewise, if we insert the items in descending order : 77, 66, 55, 44, 33, 22, 11, then our tree will be imbalanced the other way:
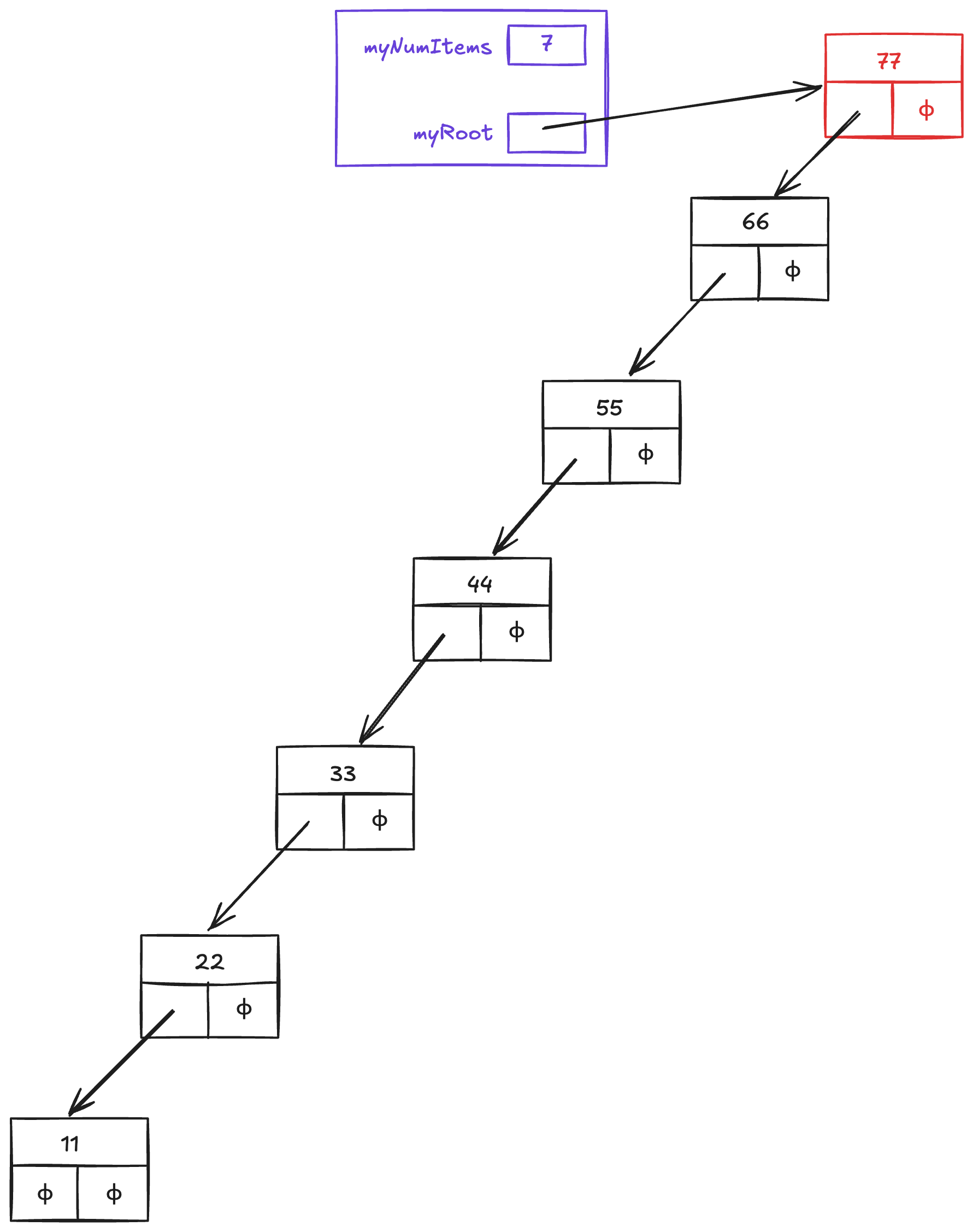
Figure 3:Imbalanced tree after inserting 77, 66, 55, 44, 33, 22, 11
As before, this tree’s height is 7, its diameter is 7, and its maximum width is 1.
In tests.cpp, uncomment the TEST_CASE for “insert()”. Save/compile, and verify that you get a compilation error indicating that insert() is undeclared.
In BST.h, below the class declaration, create a stub for BST::insert() (a “stub” is code that does nothing -- it just returns) and a stub for BST::Node::insert(). Recompile, and when all errors have been eliminated, run the test. Then define both BST::insert() and BST::Node::insert() so that it passes the test.
You will need to define insert functions in both the BST class, and additionally within the Node struct within the BST class. Both will look the same!
void insert(const Item& it);Do your best to implement these two insert functions. The job of the BST::insert() function is to setup the Node tree if it doesn’t exist by making the initial node, and if the Node tree does exist, it needs to pass-the-buck to the BST::Node::insert() function to deal with it recursively. It additionally counts how many items are in the tree.
The BST::Node::insert() function needs to correctly insert the new Item it into the pre-existing Node tree recursively - checking whether it needs to be inserted correctly to the left (less than) or to the right (greater than). Our BST does not need to deal with duplicates! If a duplicate is given, we need to throw an Exception back. We have provided an Exception.h file to use for this. Once the item is recursively insert() to the place in the tree where it can be added (ie, a blank nullptr for left or right) then it will make and attach a new Node(it) to the tree and return.
If you need more help than what is provided here, there is a hint in case you get stuck. You should be able to build this method without looking at the hint though! Keep trying and rebuilding your project until the insert() section in tests.cpp passes completely.
The contains() Method¶
In tests.cpp, uncomment the TEST_CASE for contains(). Take a few minutes to look over the tests it contains, specifically how contains() is used. As can be seen, the contains(it) method returns true if it is in its BST; otherwise it returns false. Save/compile your project. You should see an error indicating that there is no method matching the calls in our test-method.
Modify BST.h as necessary to fix any compilation/linking errors, using an approach similar to the approach used in insert().
You will need to define contains functions in both the BST class, and additionally within the Node struct within the BST class. Both will look the same!
bool contains(const Item& it) const;Do your best to implement these two contains functions. If you get stuck, here is a hint, but don’t use it unless you have to. You should be able to build this method without looking at the hint! Keep trying and rebuilding your project until the contains() section in tests.cpp passes completely.
Continue when your method passes the test.
Three Traversal Methods¶
To traverse a data structure is to pass through each of its items, processing each item in turn. For example, outputting the values in an array, vector, or list usually involves traversing the structure and outputting each item in turn.
When it comes to binary search trees, there are a variety of ways to traverse a BST:
A preorder traversal “processes” the item in a node before the items in the left and right subtrees are (recursively) processed.
A postorder traversal “processes” the item in a node after the items in the left and right subtrees are (recursively) processed.
An inorder traversal “processes” the item in a node after the items in the left subtree have been processed, but before the items in the right subtree have been (recursively) processed.
To illustrate, the BST class template contains a traversePreorder() method, defined as follows:
void BST::traversePreorder(ostream &out) const {
if (!isEmpty()) {
myRoot->traversePreorder(ostream &out);
}
}If the BST is not empty, this method “passes the buck” by sending the traversePreorder() message to the node whose address is in myRoot. The Node struct defines that (recursive) method as follows:
void BST::Node::traversePreorder(ostream &out) const {
// 1. process myItem first (preorder)
processItem(out);
// 2. then recursively process the items in the left subtree
if (myLeft != nullptr) {
myLeft->traversePreorder(out);
}
// 3. then recursively process the items in the right subtree
if (myRight != nullptr) {
myRight->traversePreorder(out);
}
}The processItem() method can be defined to do any kind of processing of a node’s item. To illustrate, our Node struct defines processItem() to insert a space and then myItem into cout:
void BST::Node::processItem(ostream &out) {
out << myItem << ' ';
}Note that all of these functions take an ostream as a parameter and pass it on in their method calls. The processItem() method writes its output to the ostream. By passing in an output stream this way, the caller can have processItem write to standard out (cout) or a file (fout) or even a string, which is what test.cpp does.
Uncomment the TEST_CASE for traversal, and take a moment to look over its tests. Your final task is to define traversePostorder() and traverseInorder() methods that will produce the output expected by the test-method. Use the provided traversePreorder() methods as a model; the other two sets of traversal methods are quite similar.
When your code passes all the tests, congratulations! You now have a basic binary search tree class!
Submit¶
Grading Rubric: 25 points total
5 pts:
insert()correct5 pts:
contains()correct4 pts x 3 = 12 pts: traversals are correct
3 pts: code is neat and clean (hospitable)
Ways students lost points in the past:
-1:
Node::containshas to RETURN the value gotten from recursive calls of contains-2:
insert()should be recursive;-1:
insert()should throw an exception when item is already in tree-2: very poor indentation
-2:
traversePostorderandtraverseInordershould call themselves, not traversePreorder-2:
Node::traverseInOrderneeds to process item in the middle (and useprocessItemmethod) insert